红黑树
红黑树是平衡二叉树的一种实现,它追求局部平衡,插入、删除复杂度都为 O(Logn),它在插入和删除操作上比AVL树更优秀。它具有以下性质:
- 每个节点颜色为红色或者黑色。
- 根节点为黑色
- 整棵树中不存在相邻的红色节点
- 从树中的每个节点到它的任意叶子节点经过的黑色节点数量相同。
插入操作
红黑树中采用两方法来平衡树,分别为:染色、旋转。
假设新插入的节点为X
-
采用二分查找新节点插入位置并设置新节点为红色(为黑色不能满足第四点性质)。
-
如果x为根节点,重置x颜色为黑色。
-
如果x父节点是黑色,直接插入。
-
如果x父节点是黑色,按如下方式操作:
1、如果x的叔节点是红色
(1)该变x的父节点和叔节点的颜色为黑色
(2)将祖父节点颜色设为红色
(3)对祖父节点重复上面两个步骤
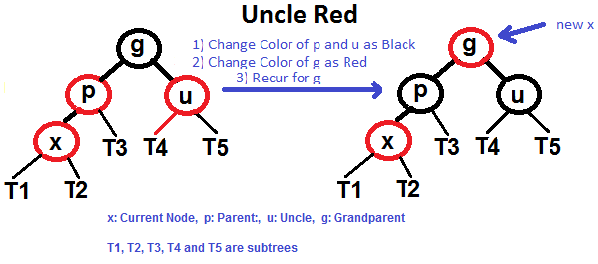
2、如果x的叔节点是黑色或空,对x节点的操作分四种情况,和对AVL树的做类似的旋转操作。
(1)左左情况(新插入节点为父节点的左孩子,父节点为祖父节点的左孩子)
(2)左右情况(新插入节点为父节点的左孩子,父节点为祖父节点的右孩子)
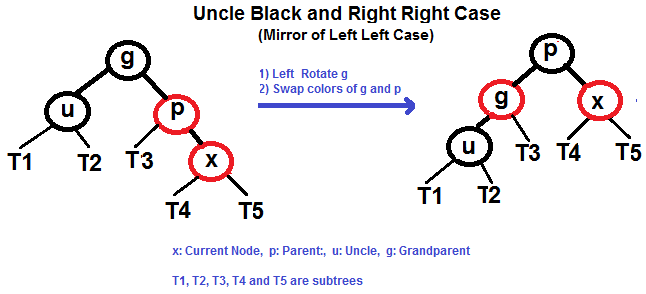
(3)右左情况(新插入节点为父节点的右孩子,父节点为祖父节点的左孩子)
(4)右右情况(新插入节点为父节点的右孩子,父节点为祖父节点的右孩子)
左左情况操作
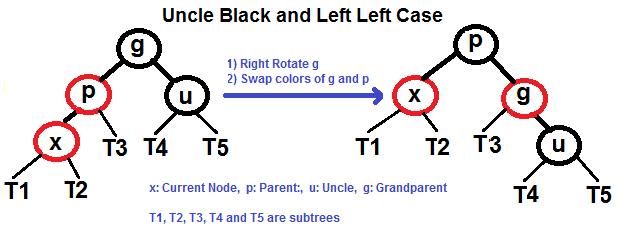
左右情况操作
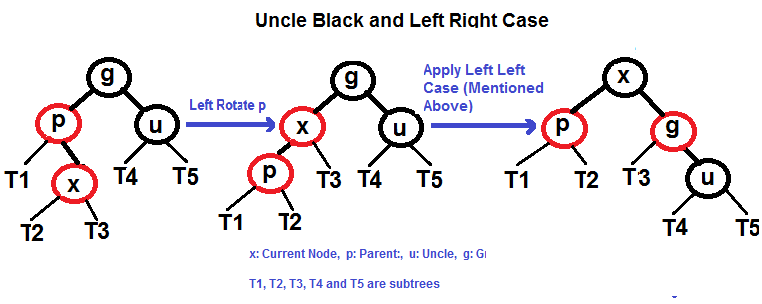
右左情况操作
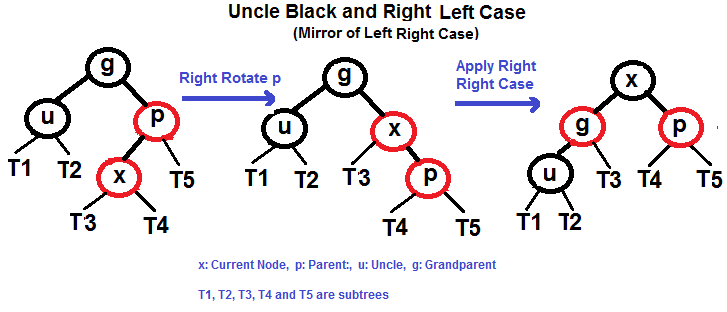
右右情况操作