平衡二叉树
AVL树是最早提出的平衡二叉树,它基本性质就是:左右子树的高度差不超过1,且左右子树都是一颗平衡二叉树。
旋转
AVL树通过旋转平衡左右子树高度,它有四种基本的旋转方式,分别为:左旋转,右旋转,左右转载,右左旋转。
右旋转
右旋:即用左儿子取代根,假设我们要旋转以X为根,LR分别为X的左右儿子,那么我们只需要把L的右儿子取代X的左儿子,然后把更新后的X赋值为L的右儿子,就可以了。
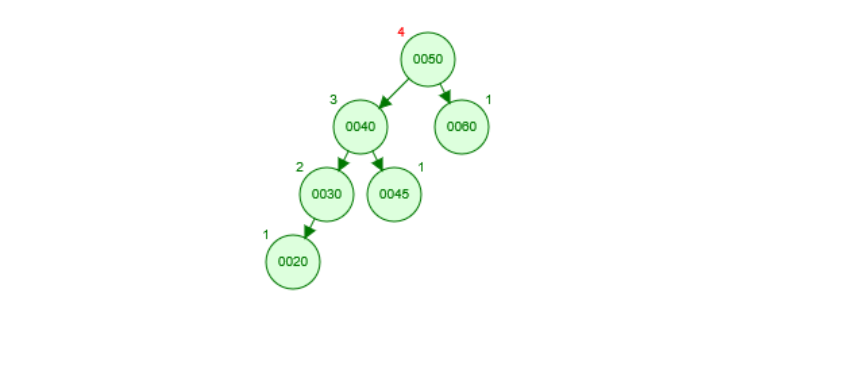
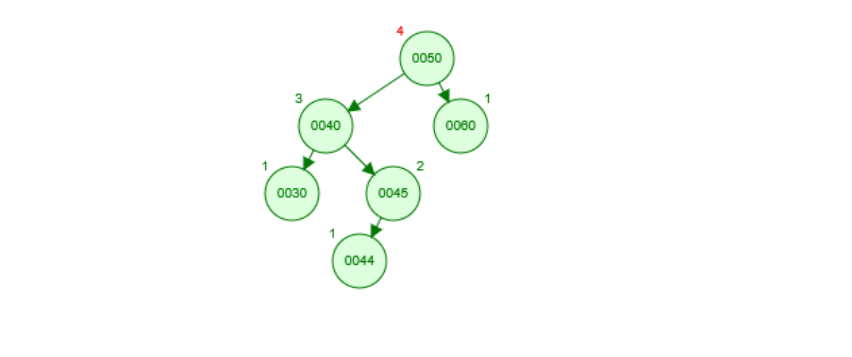
假设待调节的平衡二叉树如下图所示。
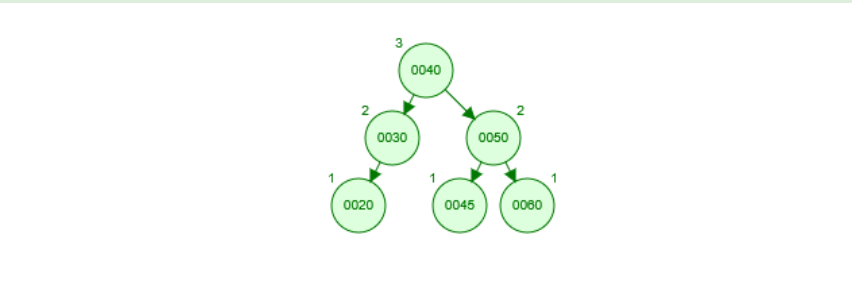
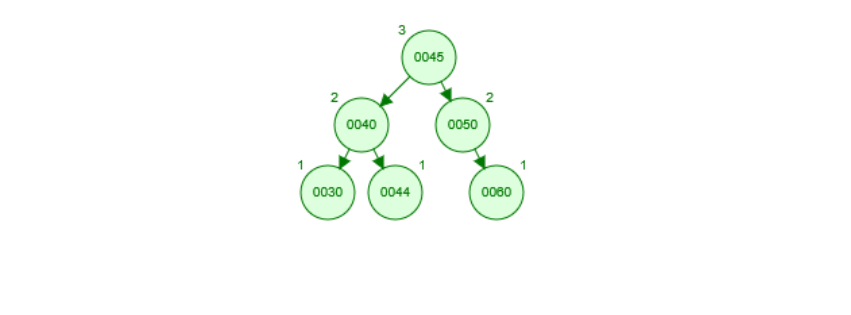
右旋调整结果如下图所示
左旋转
左旋:即用右儿子取代根,假设我们要旋转以X为根,LR分别为X的左右儿子,那么我们只需要把R的左儿子取代X的右儿子,然后把更新后的X赋值为R的左儿子,就可以了。
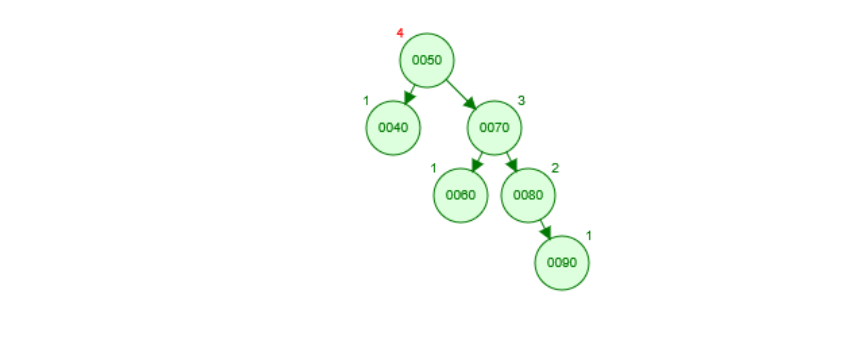
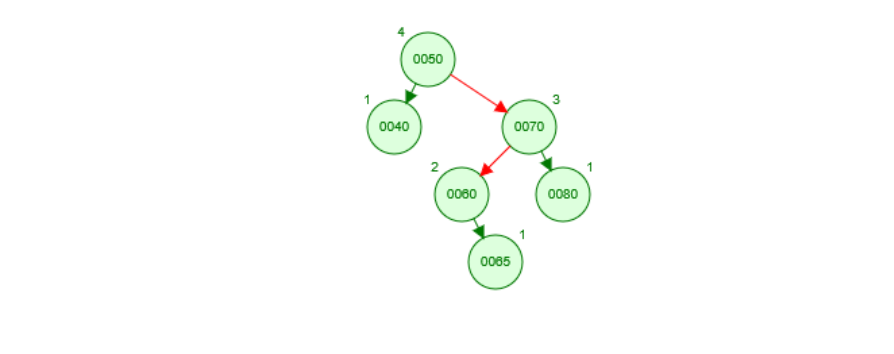
假设有待调整树形如下图所示:
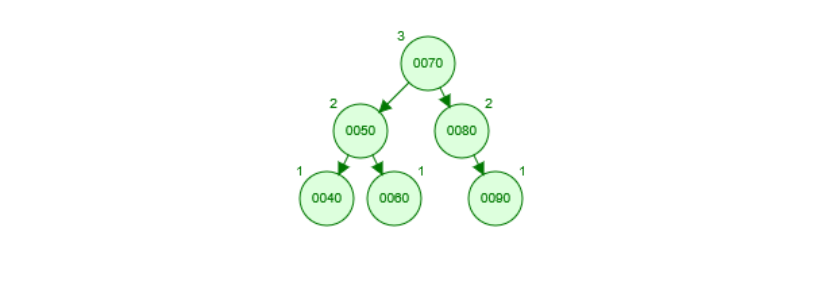
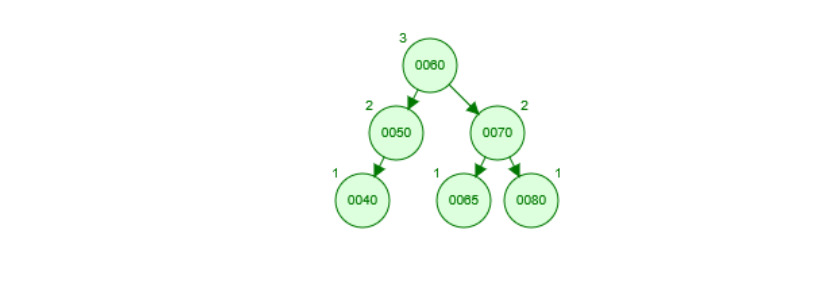
左旋转后的树形如图下所示:
左右旋
对于出现根的左子树较根的右子树高且新插入节点是根的左子树的右子树,单独的右旋操作并不会降低树的高度,必须先左旋根节点的左子树,再整体右旋。事实上先左旋根的左子树是为了提高左子树的高度,然后以整树右旋达到左右子树平衡。
假设有待调整树形如下图所示:
左右旋转后调整树形如下所示:
右左旋转
情况与左右旋转类似:先右旋根节点的右子树,再整体左旋。
假设有待调整树形如下图所示:
右左旋转后调整树形如下所示:
右旋转 && 左右旋转
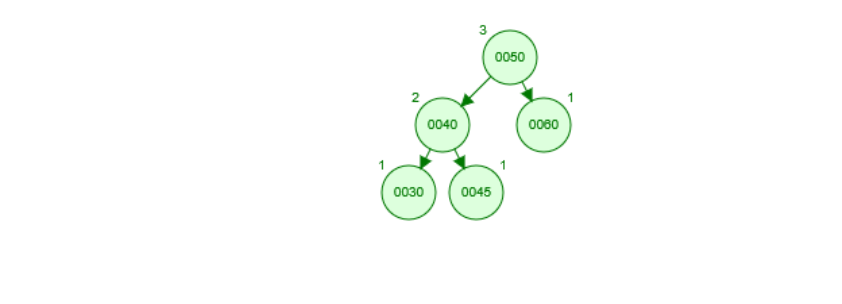
假设我们有以下平衡二叉树如图所示:当我们插入的新节点在 ㉚ 下面时候, 此时以50为根节点的树失衡,同时以40为根节点的树的左子树高度比它的右子树高, 这种失衡情况只需要右旋整树;当我们呢插入的新节点在45下面是,此时以50为根节点的树失衡, 且以40为根节点的左子树高度小于右子树高度,这个时候要左旋以40为根节点的树(增高左子树),右旋整树 ,所以推导出:
当Hight(root->left) - High(root->right) > 1, High(root->left->left) > High(root->left->right), 右旋。
当Hight(root->left) - High(root->right) > 1, High(root->left->left) > High(root->left->right), 左右旋。
同理可以推导出右子树的情况:
High(root->right) - Hight(root->left) > 1, High(root->right->right) > High(root->right->left), 左旋
High(root->right) - Hight(root->left) > 1, High(root->right->right) < High(root->right->left),右左旋
删除
1、按照二叉排序树的删除节点方法删除
2、回溯节点时候判断是否发生失衡,是的话即按照上面判断旋转方法调整失衡。