题意
平面坐标系中,给定一矩形四点和一点的坐标,如何该点是否在矩形内。
叉乘
叉乘又称为外积,它的运算结果是一个向量而不是一个标量,向量的叉乘有有以下性质。
a^b = -b^a
|c| = |a^b| = |a|*|b|*sin<a,b>
叉乘的结果a^b是a和b所在平面的法向量,它的方向是垂直a和b所在的平面,并且按照a、b和a^b的次序构成右手法则,所以叉乘的另一个性质可以通过它的符号判断两个向量之间的位置关系是顺时针还是逆时针,具体如下。
1、a^b这个向量的系数为正,则a在b的顺时针方向。
2、a^b这个向量的系数为负,则a在b的逆时针方向。
3、a^b等于0,a和b共线。
判断
1、 构造四个三角形是否等于矩形面积来判断,计算比较多。叉乘判断更简洁。
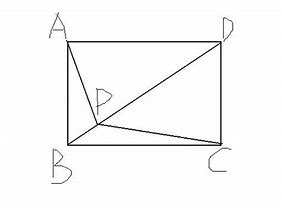
2、于点在矩形内,分别判断点是否在平行的两个线段之间。下图中,判断P分别在线段AP和CD之间,在线段BC和AD之间, 那边向量BP和CP对于向量AB而已方向肯定是一个顺时针一个逆时针。
就有:(BA^BP )(CD^CP) <= 0 && (BC^BP)(AD^AP) <= 0